Construct Binary Tree from Preorder and Inorder Traversal

Introduction

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Things you should know

1. Traversal of a Tree

In tree traversal algorithms, Depth-First Search (DFS) can be performed in three main ways: preorder, inorder, and postorder. In contrast, Breadth-First Search (BFS) uses a method called level-order traversal, where you explore nodes level by level, starting with the parent nodes and then their children. 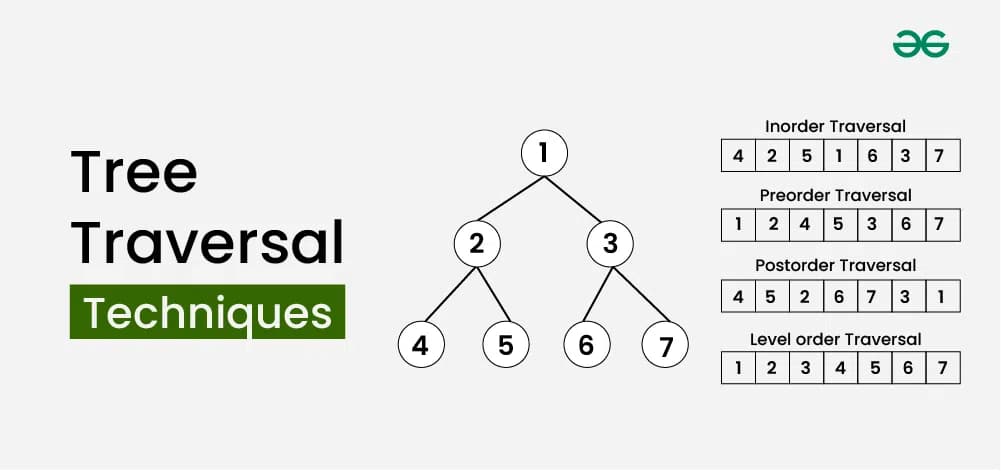tree traversal

Solutions

1. Using DFS (Recursion)

The implementation is rather simple; it's the underlying idea that matters. To build a binary tree from its preorder and inorder traversal sequences using DFS and recursion, we can follow these steps:

Preorder Traversal Insight: In preorder traversal, the first element is always the root of the tree or subtree. By repeatedly taking the first element from the preorder list, we can determine the root of the current subtree.
Inorder Traversal Insight: In inorder traversal, elements to the left of the root are part of the left subtree, and elements to the right are part of the right subtree. Using the root element found in the preorder list, we can split the inorder list into left and right subtrees. Recursive Construction:

main.py

def build_tree(preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
    if inorder:
        index = inorder.index(preorder.pop(0))
        node = TreeNode(inorder[index])
        node.left = build_tree(preorder, inorder[:index])
        node.right = build_tree(preorder, inorder[index+1:])
        return node

Introduction

Things you should know

1. Traversal of a Tree

Solutions

1. Using DFS (Recursion)

References